E91 Protocal是Artur Ekert於1991年提出的。
他是基於糾纏光子的兩個特性:

1. 完美相關聯
2. 任何嘗試都會使量子位塌縮並破壞EPR狀態。

量子糾纏

糾纏是指兩個粒子之間的一種特殊聯繫，無論糾纏粒子彼此之間有多遠，一旦測量了一個粒子，你就可以立即知道第二個粒子的值。

但這要怎麼驗證?第二個粒子如何知道第一個粒子是否被測量以及它的值是多少？

這有兩種解釋

• 第一個可能的解釋是，兩個粒子都處於持續且直接的通訊中。但在這種情況下，粒子之間的通訊比光更快。但這是有問題的，因為它違反了愛因斯坦的狹義相對論！
• 第二種解釋是，當糾纏粒子產生時，它們都嵌入了隱藏變數。這些隱藏的變數精確地控制著這些粒子一生的行為。

由於第一種解釋違反了狹義相對論，著名物理學家愛因斯坦、波多爾斯基和羅森支持第二種理論，並表示一定存在隱藏參數。

但貝爾不等式或貝爾測試，表明不可能存在隱藏參數！
2022年諾貝爾物理學獎就是與這一點的實驗驗證有關。

Bell State

以下狀態稱為Bell State、EPR State 或是 EPR 對。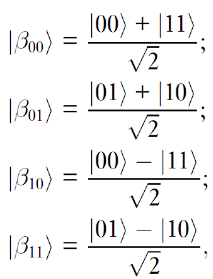

透過以下量子電路便可以創建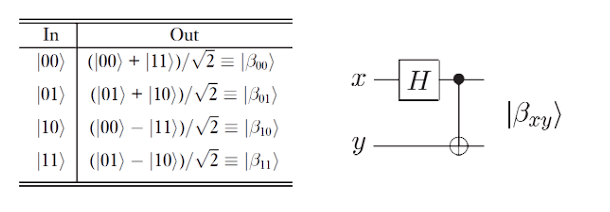

Bell test

假設我們將一對糾纏的粒子分給Asja和Balvis，他們手中各有一個處於糾纏狀態的粒子。
他們將使用W-base進行測量
W-base是Z軸旋轉pi/4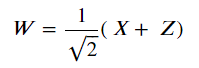

隱藏參數

假設隱藏參數的理論是對的，那麼參數控制著我們的量子位元在被某些測量base偵測到時的行為。
在實驗中，我們有X、Z、W-base，每個量子位元都有一些參數，這些參數將確定每個測量基礎
是否會檢測到它（Y）或檢測不到（N ）。
因此下面的組合都是有可能的:

如果 Asja 和 Balvis 選擇不同的測量基礎，他們將能夠在部分情況中獲得相同的結果（當Y時將檢測到量子位，而當N時不會檢測到量子位元）。
我們感興趣的是他們選擇不同的基礎並得到不同結果的情況：

• Asja決定 𝑍 base，Balvis選擇 𝑋（或相反亦然）
• Asja決定 𝑋 base，Balvis選擇 𝑊（或相反亦然）
• Asja決定 𝑊 base，Balvis選擇 𝑍（或相反亦然）

根據上表，對於每個可能的隱藏參數設置，我們可以評估 Asja 和 Balvis 是否能夠獲得相同的S(same)或不同的D(different)結果。
因此，我們可以建立一個新的表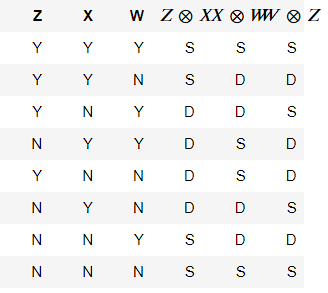

因此，在 24 個案例中的 12 個案例中，Asja 和 Balvis 將能夠獲得相同的S結果（50%)

用程式來驗證隱藏參數

從 EPR 對開始。
每個場景運行 100 輪，計算使用者獲得相同結果的輪次11或者00:

• Asja 測量了第一個粒子 𝑍 base上，巴爾維斯測量了第二個粒子𝑋 base。
• Asja 測量了第一個粒子 𝑋 base上，巴爾維斯測量了第二個粒子 𝑊 base。
• Asja 測量了第一個粒子 𝑊 base上，巴爾維斯測量了第二個粒子 𝑍 base。
  Note：將測量base旋轉到 𝑊-axis，需使用Gate序列： 𝑆 - 𝐻 − 𝑇 - 𝐻

在量子電路中建立貝爾態或 EPR 對，我們的預測是，使用者在執行 300 輪後應該會獲得相同結果 ≤ 150 次。

# import all necessary objects and methods for quantum circuits
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from random import randrange

#choosing Z and X bases
qreg = QuantumRegister(2) 
creg = ClassicalRegister(2) 
mycircuit1 = QuantumCircuit(qreg, creg)
    
#Creating entanglement
mycircuit1.h(qreg[0])
mycircuit1.cx(qreg[0], qreg[1])
    
#asja measures 1st qubit qreg[0] in Z basis, thus do nothing
    
#balvis measures 2nd qubit qreg[1] in X basis, thus applies H gate first
mycircuit1.h(qreg[1])
mycircuit1.draw(output="mpl")

mycircuit1.measure(qreg,creg)

job = execute(mycircuit1,Aer.get_backend('qasm_simulator'),shots=100) #100 rounds
countsZX = job.result().get_counts(mycircuit1) # counts is a dictionary object in python

print(countsZX)

{'10': 28, '01': 20, '00': 27, '11': 25}

#choosing X and W bases

qreg = QuantumRegister(2) 
creg = ClassicalRegister(2) 
mycircuit2 = QuantumCircuit(qreg, creg)
    
#Creating entanglement
mycircuit2.h(qreg[0])
mycircuit2.cx(qreg[0], qreg[1])
  
#asja measures 1st qubit qreg[0] in X basis, thus applies H gate first
mycircuit2.h(qreg[0])
    
#balvis measure 2nd qubit qreg[1] in W basis, thus applies S-H-T-H gates first
mycircuit2.s(qreg[1])
mycircuit2.h(qreg[1])
mycircuit2.t(qreg[1])
mycircuit2.h(qreg[1])
    
mycircuit2.draw(output="mpl")

mycircuit2.measure(qreg,creg)

job = execute(mycircuit2,Aer.get_backend('qasm_simulator'),shots=100) #100 rounds
countsXW = job.result().get_counts(mycircuit2) # counts is a dictionary object in python

print(countsXW)

{'11': 37, '00': 47, '10': 11, '01': 5}

#choosing W and Z bases
qreg = QuantumRegister(2) 
creg = ClassicalRegister(2) 
mycircuit3 = QuantumCircuit(qreg, creg)
    
#Creating entanglement
mycircuit3.h(qreg[0])
mycircuit3.cx(qreg[0], qreg[1])
    
#asja measure 1st qubit qreg[0] in W basis, thus applies S-H-T-H gates first
mycircuit3.s(qreg[0])
mycircuit3.h(qreg[0])
mycircuit3.t(qreg[0])
mycircuit3.h(qreg[0])
    
#balvis measure 2nd qubit qreg[1] in Z basis, thus do nothing

mycircuit3.draw(output="mpl")

mycircuit3.measure(qreg,creg)

job = execute(mycircuit3,Aer.get_backend('qasm_simulator'),shots=100) #100 rounds
countsWZ = job.result().get_counts(mycircuit3) # counts is a dictionary object in python
    
print(countsWZ)

{'11': 43, '00': 39, '10': 10, '01': 8}

#We are interested in rounds where Asja and Balvis got same results "00" or "11"
sameZX=countsZX.get('00')+countsZX.get('11')
sameXW=countsXW.get('00')+countsXW.get('11')
sameWZ=countsWZ.get('00')+countsWZ.get('11')

totalSame=sameZX+sameXW+sameWZ

print('Users received same result in', totalSame, 'out of 300 rounds')

Users received same result in 218 out of 300 rounds

我們的實驗結果不支持這個預測！
因此，貝爾測試表明不能存在隱藏變量，因為如果存在這樣的變量來確定光子是否會通過特定的門，我們期望用戶每隔一段時間就能得到相同的結果（≤150)，然而實驗結果相反。

貝爾定理指出「局部隱變數的物理理論無法重現量子力學的所有預測」。

EPR理論的目標是透過證明量子力學缺乏一些基本的「現實元素」來證明量子力學是不完整的。

貝爾測試表明，大自然透過實驗證明了這一觀點無效，同時與量子力學一致！

參考資料: Womanium 教材